This page was generated from docs/examples/4_anomalousmap.ipynb. Interactive online version: .

Anomalous Difference Map

In Basics, we loaded a room-temperature dataset that was collected at ~6550 eV of tetragonal HEWL. We then computed the \(CC_{1/2}\) and \(CC_{anom}\) for this data in Merging Statistics and observed that there was significant anomalous signal. Let’s now use that data to generate an anomalous difference map based on the anomalous scattering from the native sulfur atoms.

import reciprocalspaceship as rs
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context("notebook", font_scale=1.3)
import numpy as np

print(rs.__version__)

0.10.3

# Load data and extract relevant columns
refltable = rs.read_mtz("data/HEWL_SSAD_24IDC.mtz")
refltable = refltable[["I(+)", "SIGI(+)", "I(-)", "SIGI(-)", "N(+)", "N(-)"]]
refltable.head()

			I(+)	SIGI(+)	I(-)	SIGI(-)	N(+)	N(-)
H	K	L
0	0	4	661.29987	21.953098	661.29987	21.953098	16	16
		8	3229.649	105.980934	3229.649	105.980934	16	16
		12	1361.8672	43.06085	1361.8672	43.06085	16	16
		16	4124.393	196.89108	4124.393	196.89108	8	8
1	0	1	559.33685	8.6263	559.33685	8.6263	64	64

print(f"Number of reflections: {len(refltable)}")

Number of reflections: 12542

---

Background

Since this dataset was collected at a single wavelength, we can compute an anomalous difference map from the anomalous structure factor amplitudes, \(|F_{A}|\), and their phase shifts, \(\alpha\), relative to the computed phases from an isomorphous structure of tetragonal HEWL. We will compute \(|F_{A}|\) based on the following:

\begin{equation*} |F_{A}| \propto \Delta_{\mathrm{ano}} = |F_{HKL}| - |F_{\overline{HKL}}| \end{equation*}

We will then use a model refined from this data to obtain the phases, \(\phi_c\), which can be used to determine the phases for the anomalous contribution, \(\phi_A\), using the phase shift, \(\alpha\):

\begin{equation*} \phi_A = \phi_c - \alpha \end{equation*}

Since this is a SAD experiment, we can assume \(\alpha\) is 90˚ when \(\Delta_{\mathrm{ano}}\) is negative and 270˚ when it is positive. This formalism is based on Thorn and Sheldrick, J Appl. Cryst. (2011).

---

Computing Structure Factor Amplitudes

The dataset being used is the direct output from running scaling and merging in AIMLESS. As a first processing step, we need to convert the observed merged intensities, \(I(+)\) and \(I(-)\), into observed structure factor amplitudes, \(F(+)\) and \(F(-)\).

# Stack intensities from 2-column anomalous to 1-column format
stacked = refltable.stack_anomalous()
stacked = stacked.loc[stacked["N"] > 0]
stacked.sort_index(inplace=True)
stacked.head()

			I	SIGI	N
H	K	L
-45	-10	-1	6.185645	2.932488	4
	-9	-2	27.028767	3.8457258	4
		-1	3.0018542	2.6649861	4
	-8	-3	-0.9806365	2.7741797	4
		-2	12.085027	3.0270035	4

In order to get structure factor amplitudes, we must first account for mean intensities that are negative due to background subtraction. We will use a method based on the Bayesian approach first proposed by French and Wilson to ensure that all intensities are strictly positive. This method is implemented in rs.algorithms.scale_merged_intensities().

scaled = rs.algorithms.scale_merged_intensities(stacked, "I", "SIGI",
                                                mean_intensity_method="anisotropic")

scaled.head()

			I	SIGI	N	dHKL	CENTRIC	FW-I	FW-SIGI	FW-F	FW-SIGF
H	K	L
-45	-10	-1	6.185645	2.932488	4	1.7194302	False	6.1471047	2.7739754	2.4032679	0.6094333
	-9	-2	27.028767	3.8457258	4	1.7217722	False	26.716537	3.8457258	5.1551414	0.37557602
		-1	3.0018542	2.6649861	4	1.7271528	False	3.5474997	2.1485696	1.7800175	0.6156602
	-8	-3	-0.9806365	2.7741797	4	1.7197413	False	1.8468517	1.4775624	1.2411455	0.5535428
		-2	12.085027	3.0270035	4	1.7287054	False	11.893286	3.02595	3.4186602	0.45392564

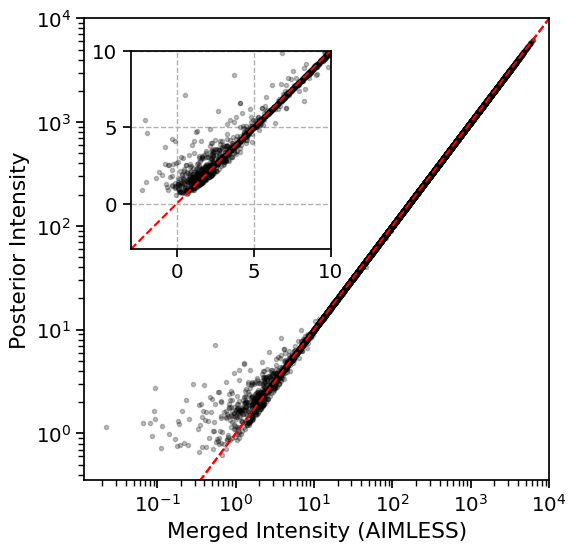
French-Wilson scaling leaves large intensities relatively unchanged, but rescales negative and small intensities to be positive by imposing Wilson’s distribution as a prior:

x = np.linspace(-3, 10000, 2)
plt.figure(figsize=(6, 6))
ax = plt.gca()
plt.plot(x, x, '--r', scalex=False, scaley=True)
plt.plot(scaled["I"].to_numpy(), scaled["FW-I"].to_numpy(), "k.", alpha=0.25)
plt.plot(plt.xlim(), plt.xlim(), '--r', scalex=False, scaley=True)
plt.xlabel("Merged Intensity (AIMLESS)")
plt.ylabel("Posterior Intensity")
plt.xscale("log")
plt.yscale("log")
plt.xlim(right=1e4)
plt.ylim(top=1e4)

# Inset
axins = ax.inset_axes([0.1, 0.5, 0.43, 0.43])
axins.plot(scaled["I"].to_numpy(), scaled["FW-I"].to_numpy(), "k.", alpha=0.25)
axins.plot(x, x, '--r')
axins.set_xlim(-3, 10)
axins.set_ylim(-3, 10)
axins.grid(linestyle="--")

plt.show()

# Remove extra columns
scaled = scaled[["FW-F", "FW-SIGF", "N"]]

# "Unstack" anomalous data from one-column to two-column format
anom = scaled.unstack_anomalous(["FW-F", "FW-SIGF", "N"]).dropna()

anom.head()

			FW-F(+)	FW-SIGF(+)	N(+)	FW-F(-)	FW-SIGF(-)	N(-)
H	K	L
0	0	4	25.7036	0.4273095	16	25.7036	0.4273095	16
		8	56.794975	0.93358195	16	56.794975	0.93358195	16
		12	36.885887	0.5840336	16	36.885887	0.5840336	16
		16	64.02966	1.5395098	8	64.02966	1.5395098	8
1	0	1	23.647089	0.18242109	64	23.647089	0.18242109	64

# Compute differences
dF    = np.abs(anom["FW-F(+)"] - anom["FW-F(-)"])
sigDF = np.sqrt(anom["FW-SIGF(+)"]**2 + anom["FW-SIGF(-)"]**2)
anom["ANOM"] = rs.DataSeries(dF, dtype="SFAmplitude")
anom["SigANOM"] = rs.DataSeries(sigDF, dtype="Stddev")

anom.head()

			FW-F(+)	FW-SIGF(+)	N(+)	FW-F(-)	FW-SIGF(-)	N(-)	ANOM	SigANOM
H	K	L
0	0	4	25.7036	0.4273095	16	25.7036	0.4273095	16	0.0	0.60430694
		8	56.794975	0.93358195	16	56.794975	0.93358195	16	0.0	1.3202842
		12	36.885887	0.5840336	16	36.885887	0.5840336	16	0.0	0.82594824
		16	64.02966	1.5395098	8	64.02966	1.5395098	8	0.0	2.1771955
1	0	1	23.647089	0.18242109	64	23.647089	0.18242109	64	0.0	0.25798237

---

Phasing the Anomalous Difference Map

Below, we will compute the necessary phase shifts to go from the phases of a \(2 F_o - F_c\) map to the phases associated with the anomalous difference structure factors. Although this model was refined to this data in PHENIX, the phases from any isomorphous structure could have been used to obtain a reasonable map.

ref = rs.read_mtz("data/HEWL_refined.mtz")

# Find common HKL indices
hkls = anom.index.intersection(ref.index).sort_values()
anom = anom.loc[hkls]

As mentioned in Background, we can compute the anomalous phases as follows:

\begin{equation*} \phi_A = \phi_c - \alpha \end{equation*}

where \(\alpha\) is 90˚ when \(\Delta_{\mathrm{ano}}\) is negative and 270˚ when it is positive.

alpha = 90 + 180*(anom["FW-F(+)"] >= anom["FW-F(-)"])
anom["PHANOM"] = ref.loc[hkls, "PH2FOFCWT"] + alpha
anom["PHANOM"] = rs.utils.canonicalize_phases(anom["PHANOM"]).astype("Phase")

Viewing the Map

Since we have structure factor amplitudes, anom["ANOM"], and phases, anom["PHANOM"], for the anomalous structure factors, we can now view the anomalous difference map. This can be done by writing out an MTZ file, and loading it into COOT, PyMOL, or any other molecular graphics package.

anom.dtypes

FW-F(+)       FriedelSFAmplitude
FW-SIGF(+)       StddevFriedelSF
N(+)                      MTZInt
FW-F(-)       FriedelSFAmplitude
FW-SIGF(-)       StddevFriedelSF
N(-)                      MTZInt
ANOM                 SFAmplitude
SigANOM                   Stddev
PHANOM                     Phase
dtype: object

anom.write_mtz("data/anomdiff.mtz")

Looking at the anomalous difference map on the refined structure, we can see positive difference density on all of the sulfurs in HEWL (shown below in purple):

%%html
<center>
    <iframe src="https://rs-station.github.io/reciprocalspaceship/data/anomdiff/anomdiff.html#zoom=25", width=600, height=600></iframe>
    <br>Anomalous difference map from HEWL crystal overlayed with refined model (PDB: 7L84). Map is contoured at +5&sigma;.
</center>

Anomalous difference map from HEWL crystal overlayed with refined model (PDB: 7L84). Map is contoured at +5σ.